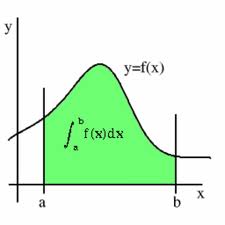
Una integral es una suma de infinitos sumandos, infinitamente pequeños.
La integral de una función se utiliza principalmente para el cálculo de áreas y volúmenes de regiones y sólidos de revolución. Si una función tiene una integral, se dice que es integrable. De la función de la cual se calcula la integral se dice que es el integrando. Se denomina dominio de integración a la región sobre la cual se integra la función
Sea f(x) una función continua en el intervalo [a, b]. A partir de esta función se define la función integral:
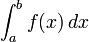
Propiedades de la integral:
f + g es integrable → ∫(f + g) = ∫f + ∫g
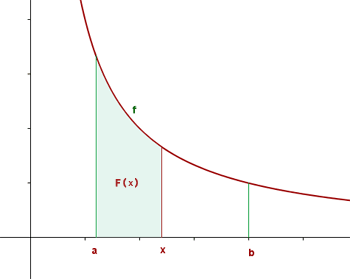
Entonces el área bajo la curva es:
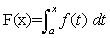
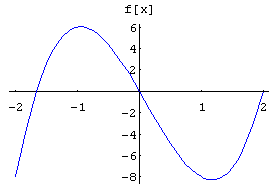
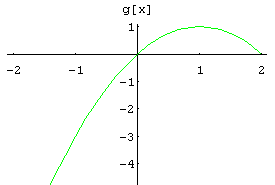
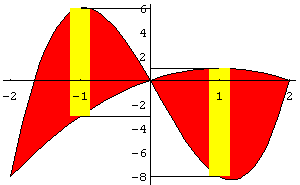
El área entre las gráficas de y=f(x) , y=g(x) en el intervalo [a,b] está dado por el valor de la Integral Definida de |f-g| en [a,b].
Vía: Wikipedia
